Sistema de ecuaciones lineales
¿ Que es un sistema de Ecuación Lineal?
En matemáticas y álgebra lineal, un sistema
de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o
simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un
sistema de ecuaciones en donde cada ecuación es de primer grado), definidas
sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de
ecuaciones sería el siguiente:
En los sistemas de ecuaciones, se debe
buscar los valores de las incógnitas, con los cuales, al reemplazar, deben dar
la solución planteada en ambas ecuaciones.
A cada una de las ecuaciones se les
denomina también restricciones o condiciones.
Todo sistema de ecuaciones lineales con dos
incógnitas, x e y, tiene las siguientes representaciones:
Donde x e y son las incógnitas, y a,b,c,d,e
y f son coeficientes reales (ℝ).
Las incógnitas establecidas en un sistema
representan el punto donde se intersectan las rectas en un plano cartesiano
(x,y).
¿Qué es un plano cartesiano?
Por si no lo recuerdas, un plano cartesiano
son 2 rectas numéricas perpendiculares, una horizontal y otro vertical que se
cortan en un punto llamado origen o cero del sistema
La finalidad del plano cartesiano es
describir la posición o ubicación de un punto en el plano, la cual está
representada por el sistema de coordenadas.
El plano cartesiano también sirve para
analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la
línea, la circunferencia y la elipse, las cuales forman parte de la geometría
analítica.
Hay unos pocos métodos diferentes de
resolver sistemas de ecuaciones lineales:
El método gráfico
Este es útil cuando solo
necesita una respuesta aproximada, o está bastante seguro que la intersección
ocurre en coordenadas enteras. ¡Solo grafique las dos rectas, y vea donde se intersecan!
Aunque
en la realidad rara vez surgen problemas únicamente con dos o tres variables de
decisión resulta, sin embargo, muy útil esta metodología de resolución. Al
reproducir gráficamente las situaciones posibles como son la existencia de una
solución óptima única, soluciones óptimas alternativas, la no existencia de
solución y la no acotación, constituye una ayuda visual para interpretar y
entender el algoritmo del método Simplex (bastante más sofisticado y abstracto)
y los conceptos que lo rodean.
El método de sustitución
Primero, resuelva
una ecuación lineal para y en términos de x . Luego sustituya esa expresión por
y en la otra ecuación lineal. Obtendrá una ecuación en x . Resuelva esta, y
tendrá la coordenada en x de la intersección. Luego sustituya x en cualquier
ecuación para encontrar la coordenada en y correspondiente. (Si es más fácil,
puede iniciar resolviendo una ecuación para x en términos de y , también -
misma diferencia!)
El Método de Reducción
Consiste en igualar los coeficientes de una
misma incógnita en ambas ecuaciones y, enseguida, sumar o restar las ecuaciones,
de modo que se eliminen los términos cuyos coeficientes se igualaron.
Este método es aconsejable cuando una misma incógnita tiene en ambas ecuaciones el mismo coeficiente (restamos las ecuaciones) o los coeficientes son iguales pero con signo opuesto (sumamos las ecuaciones).

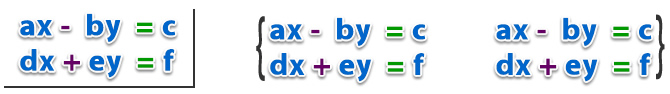
Excelente información
ResponderBorrar